JavaNetzwerktechnik

Bit Shift Operatoren in Java

Dieser Artikel geht auf die Low-Level Operatoren Left - , Right Shift und dem Logischen-Und Operator ein und erklärt an einem praxisnahen Beispiel wie diese im Detail funktionieren.

In diesem Blogbeitrag tauchen wir in die Welt der Netzwerktechnik ein und beleuchten die CIDR-Notation sowie die Berechnung von Subnetzmasken. Dabei werden wir die Grundlagen der bitweisen Operationen (Shift >>, << und AND &) erklären und ihre praktische Anwendung bei der Extraktion von IP-Oktetten demonstrieren. Der Code wird dabei Schritt für Schritt durchgegangen, um ein tieferes Verständnis für diese Techniken zu vermitteln.

Das Beispiel

Ist eine in Java implementierte Methode, die einen in CIDR Notation kodierten String, der eine IP-Adresse enthält in Subnetzmaske und IP-Adresse aufteilt und zurückt gibt.

public static String[] parseCidr(String ip) throws NumberFormatException {
    String[] addr = ip.split("/| / ");
    addr[0] = ipCheck(addr[0]);

    if (addr.length != 2) {
        return new String[] { ip };
    }

    assert addr[0] != null;
    assert addr[1] != null;

    addr[0] = addr[0].stripTrailing();
    addr[1] = addr[1].stripLeading();

    int prefix = Integer.parseInt(addr[1]);

    if (prefix < 2 || prefix > 32) {
        LOG.debug("ERROR: Prefix ausserhalb des Wertebereichs: " + prefix);
        return new String[] { ip };
    }

    int mask = 0xffffffff << (32 - prefix);
    addr[1] = String.format("%d.%d.%d.%d",
            (mask >> 24) & 0xff,
            (mask >> 16) & 0xff,
            (mask >> 8) & 0xff,
            mask & 0xff);

    return addr;
}

1. Methoden Signatur

public static String[] parseCidr(String ip) throws NumberFormatException

Diese Methode erwartet eine in CIDR Notation kodierte IP-Adresse (z.B. 192.168.1.0/24) und gibt ein Array of String zurück.

2. Entscheidende Code-Abschnitte

  • Aufteilen der IP-Adresse
String[] addr = ip.split("/| / ");

Teilt den String bei "/" oder " / " auf und erhält so ein Array aus IP-Adresse und Prefix Länge.

  • Validieren und Sanitization des Übergabeparameter
addr[0] = ipCheck(addr[0]);  // Validates IP address (method not shown)

if (addr.length != 2) {
    return new String[] { ip };  // Returns original if format invalid
}

addr[0] = addr[0].stripTrailing();
addr[1] = addr[1].stripLeading();
  • Prefix Längen Prüfung
int prefix = Integer.parseInt(addr[1]);

if (prefix < 2 || prefix > 32) {
    LOG.debug("ERROR: Prefix ausserhalb des Wertebereichs: " + prefix);
    return new String[] { ip };
}

Stellt sicher, dass das Prefix zwischen 2 und 32 liegt (gültiger Bereich für IPv4).

  • Subnetzmasken Berechnung
int mask = 0xffffffff << (32 - prefix);
addr[1] = String.format("%d.%d.%d.%d",
        (mask >> 24) & 0xff,
        (mask >> 16) & 0xff,
        (mask >> 8) & 0xff,
        mask & 0xff);

Dies ist der komplizierteste Teil:

  1. Erstellt eine 32-Bit Maske durch das Left-Shifting von Einsen (1)
  2. Konvertiert die Maske zu einem Dotted-Decimal notierten String
  3. Nutzt eine Bitwise Operation um jedes Oktett zu extrahieren
Beispiel Umwandlung
Eingabe "192.168.1.0/24"
Ausgabe ["192.168.1.0", "255.255.255.0"]

Das wird so in der Netzwerktechnik häufig verwendet, um Subnetzmasken aus der CIDR-Notation zu berechnen.

Subnetzmasken Berechnung

image

Eine Schritt für Schritt Erläuterung am konkreten Beispiel des Prefix = 24.

1. Initial Wert der Maske festlegen

int mask = 0xffffffff;
  • 0xffffff ist Hexadezimal für einen 32-Bit Wert, der alle Bits auf 1 gesetzt hat
  • In Binär: 1111 1111 1111 1111 1111 1111 1111 1111

2. Left Shift Operation

mask = 0xffffffff << (32 - prefix)
  • Für Prefix = 24:
    • 32 - 24 = 8 (Die Anzahl zu verschiebener Bits)
    • Verschiebt alle Bits nach Links um 8 Positionen weiter
    • Die neuen Bits auf der rechten Seite werden mit 0er aufgefüllt
    • Ergebnis: 1111 1111 1111 1111 1111 1111 0000 0000

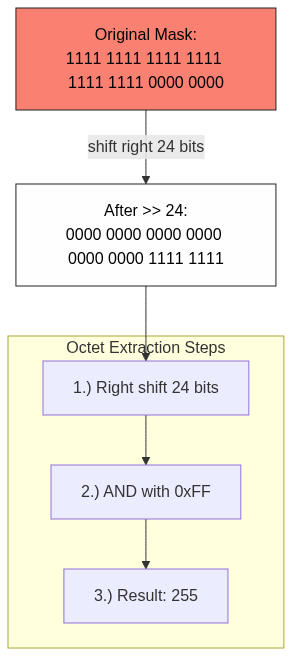
3. Die Oktette extrahieren

String.format("%d.%d.%d.%d",
    (mask >> 24) & 0xff,    // 1. Oktett
    (mask >> 16) & 0xff,    // 2. Oktett
    (mask >> 8) & 0xff,     // 3. Oktett
    mask & 0xff             // 4. Oktett
);

image

  1. Oktett: (Maske >> 24) & 0xff
    • Verschiebt 24 Bits nach rechts, um das höchstwertige Byte zu erhalten
    • AND mit 0xff, um nur die letzten 8 Bits zu erhalten
    • Ergebnis: 255
  2. Oktett: (Maske >> 16) & 0xff
    • Verschiebt 16 Bits nach rechts
    • AND mit 0xff
    • Ergebnis: 255
  3. Oktett: (Maske >> 8) & 0xff
    • Verschiebt 8 Bits nach rechts
    • AND mit 0xff
    • Ergebnis: 255
  4. Oktett: Maske & 0xff
    • Keine Verschiebung erforderlich, nur AND mit 0xff
    • AND mit 0xff
    • Ergebnis: 0

Das Endergebnis für Präfix = 24 wäre 255.255.255.0, also die Subnetzmaske für ein /24-Netzwerk.

Dieser Vorgang funktioniert für jedes Präfix zwischen 2 und 32 und erzeugt die entsprechende Subnetzmaske.

  • /16 würde Ihnen geben: 255.255.0.0
  • /28 erhalten Sie: 255.255.255.240
  • /32 würde Ihnen geben: 255.255.255.255

Die Operation & 0xff ist entscheidend, weil sie sicherstellt, dass wir nur die letzten 8 Bits (ein Byte) jedes verschobenen Ergebnisses erhalten, was für die Erstellung der gepunkteten Dezimalschreibweise einer IPv4-Adresse notwendig ist.

Beispiel für /27

1. Subnetzmasken - Berechnung /27

int mask = 0xffffffff << (32 - 27)  // Shift by 5 bits
  • Beginnend mit allen 1en: 1111 1111 1111 1111 1111 1111 1111 1111
  • Verschiebung nach links um 5: 1111 1111 1111 1111 1111 1111 1110 0000
  • Ergebnis: 255.255.255.224

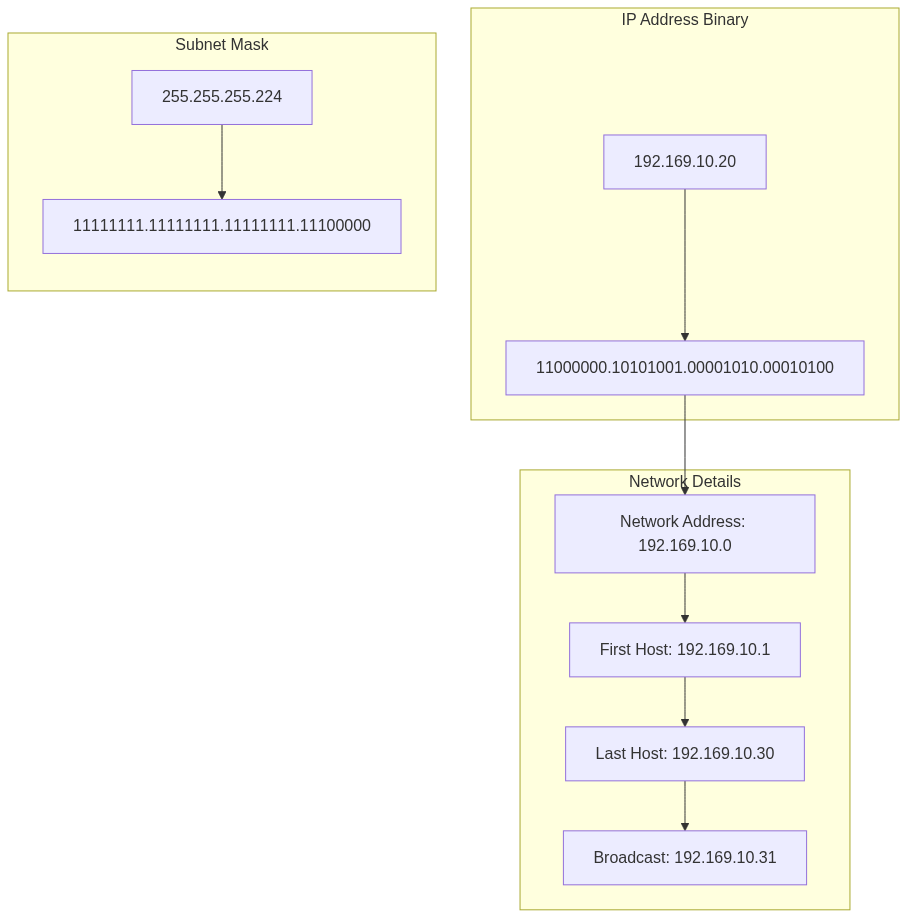
image

2. Netzwerk Informationen für 192.169.10.20/27:

  • Netzwerk Parameter
    • IP-Adresse: 192.169.10.20
    • Subnetzmaske: 255.255.255.224
    • Prefix: 27 bits
  • Binäre Aufschlüsselung:
IP Address:   11000000.10101001.00001010.00010100
Subnet Mask:  11111111.11111111.11111111.11100000
              ----------------------------------- (AND)
Network:      11000000.10101001.00001010.00000000
  • Netzwerk Detail;s
    • Netzwerk-Adresse: 192.169.10.0
      • Die erste Adresse des Netzwerks
    • Nutzbarer Host Bereich: 192.169.10.1 - 192.169.10.30
      • Mit einem /27 Präfix gibt es 32 Adressen (2^5)
      • 30 nutzbare Adressen (ohne Netzwerk und Broadcast)
    • Broadcast Adresse: 192.169.10.31
      • Das ist immer die letzte Adresse im Netzwerk

image

3. Wichtige Berechnungen

  • Netzwerk Parameter
    • IP-Adresse: 192.169.10.20
    • Subnetzmaske: 255.255.255.224
    • Prefix: 27 bits
  • Suche nach der Netzwerkadresse:
// In binary:
IP:       192.169.10.20   = 11000000.10101001.00001010.00010100
Mask:     255.255.255.224 = 11111111.11111111.11111111.11100000
Result:   192.169.10.0    = 11000000.10101001.00001010.00000000
  • Suche nach der Broadcast Adresse:
// Take network address and set all host bits to 1
Network:   192.169.10.0  = 11000000.10101001.00001010.00000000
Host bits: 5 (32-27)
Broadcast: 192.169.10.31 = 11000000.10101001.00001010.00011111

Dies zeigt, dass 192.169.10.20 Teil eines Subnetzes ist, das:

  • 32 Adressen enthält (2^5 wegen /27)
  • Eine Netz-Adresse von 192.169.10.0 hat
  • Eine Broadcast-Adresse von 192.169.10.31 hat
  • 30 nutzbare Hostadressen zulässt
  • Eine Subnetzmaske von 255.255.255.224 verwendet

Die IP-Adresse 192.169.10.20 fällt in den gültigen Hostbereich dieses Subnetzes, genauer gesagt ist es die 20. Adresse im Subnetz.

Bitwise Shift Operations

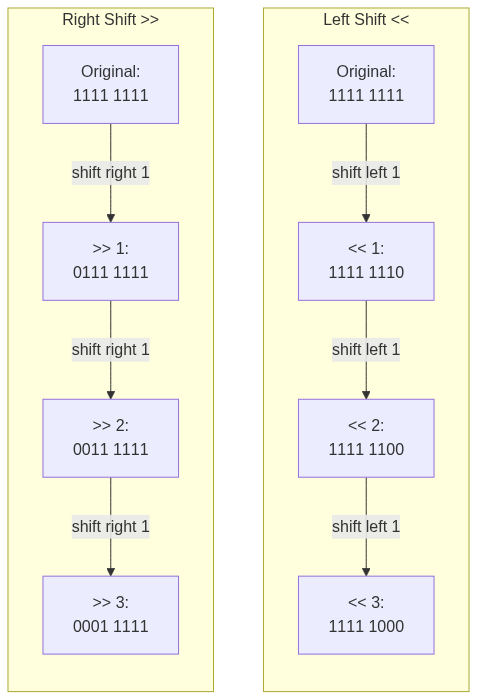
image

1. Left Shift <<

Um bei unserem Beispiel von vorhin zu bleiben: int mask = 0xffffffff << (32 - prefix)
image

Beispiel für das Prefix /24.

32 - 24 = 8 (shift amount)
0xffffffff << 8

Before: 1111 1111 1111 1111 1111 1111 1111 1111
After:  1111 1111 1111 1111 1111 1111 0000 0000

2. Right Shift >>

image

Beispiel für das Prefix /24.

// Left shift for mask creation
0xffffffff << 8  // (32-24 = 8)
Original:   1111 1111 1111 1111 1111 1111 1111 1111
Result:     1111 1111 1111 1111 1111 1111 0000 0000

// Right shifts for octet extraction
>> 24:      0000 0000 0000 0000 0000 0000 1111 1111 & 0xff = 255
>> 16:      0000 0000 0000 0000 1111 1111 1111 1111 & 0xff = 255
>> 8:       0000 0000 1111 1111 1111 1111 1111 1111 & 0xff = 255
>> 0:       1111 1111 1111 1111 1111 1111 0000 0000 & 0xff = 0

Beispiel für das Prefix /27.

// Left shift for mask creation
0xffffffff << 5  // (32-27 = 5)
Original:   1111 1111 1111 1111 1111 1111 1111 1111
Result:     1111 1111 1111 1111 1111 1111 1110 0000

// Right shifts for octet extraction
>> 24:      0000 0000 0000 0000 0000 0000 1111 1111 & 0xff = 255
>> 16:      0000 0000 0000 0000 1111 1111 1111 1111 & 0xff = 255
>> 8:       0000 0000 1111 1111 1111 1111 1111 1111 & 0xff = 255
>> 0:       1111 1111 1111 1111 1111 1111 1110 0000 & 0xff = 224

Wichtige Punkte über die Shift Operatoren:

  • Linksverschiebung (<<):

Verschiebt alle Bits um die angegebene Position nach links
Füllt die Bits ganz rechts mit Nullen auf.
Jede Verschiebung nach links multipliziert die Zahl mit 2
Wird in unserem Fall verwendet, um die Subnetzmaske zu erstellen.

  • Rechtsverschiebung (>>):

Verschiebt alle Bits um die angegebene Position nach rechts
Füllt die Bits ganz links mit Nullen auf (bei Rechtsverschiebung ohne Vorzeichen >>>)
Füllt die äußersten linken Bits mit dem Vorzeichenbit (bei vorzeichenbehafteter Rechtsverschiebung >>). Jede Rechtsverschiebung dividiert die Zahl durch 2
Wird in unserem Fall verwendet, um einzelne Oktette zu extrahieren

  • Wichtige Eigenschaften:

Die Linksverschiebung um n ist gleichbedeutend mit der Multiplikation mit 2ⁿ
Eine Rechtsverschiebung um n ist gleichbedeutend mit einer Division durch 2ⁿ.
Bits, die vom Ende weggeschoben werden, gehen verloren.
Neue Bits werden bei einer Linksverschiebung immer mit 0en aufgefüllt.
Bei der Rechtsverschiebung werden die neuen Bits auf der Grundlage des Vorzeichenbits aufgefüllt (>>-Operator).

  • Diese bitweisen Operationen sind in der Netzwerkprogrammierung wichtig für:

    • Erstellen von Subnetzmasken (Linksverschiebung)
    • Extrahieren einzelner Oktette aus IP-Adressen (Rechtsverschiebung)
    • Effiziente Durchführung von Netzwerkberechnungen
    • Manipulation von Binärdaten auf Bit-Ebene

Der logische & Operator

Ich erkläre Ihnen, wie der logische AND (&) Operator in den CIDR-Berechnungen verwendet wird, insbesondere bei der Extraktion von Oktetten aus der Subnetzmaske.

image

Betrachten wir, wie & 0xFF im Code verwendet wird:

String.format("%d.%d.%d.%d",
    (mask >> 24) & 0xff,        // Erstes Oktett
    (mask >> 16) & 0xff,        // Zweites Oktett
    (mask >> 8) & 0xff,         // Drittes Oktett
    mask & 0xff                 // Viertes Oktett
)

Lassen Sie uns dies anhand von zwei konkreten Beispielen aufschlüsseln:

  1. Beispiel mit /24 Präfix:

image

Detaillierte Aufschlüsselung für /24:

Erstes Oktett (mask >> 24) & 0xff:
    Verschoben: 0000 0000 0000 0000 0000 0000 1111 1111
    0xFF:       0000 0000 0000 0000 0000 0000 1111 1111
               ----------------------------------------------
    AND Result: 0000 0000 0000 0000 0000 0000 1111 1111 (255)

Viertes Oktett (mask & 0xff):
    Original:   1111 1111 1111 1111 1111 1111 0000 0000
    0xFF:       0000 0000 0000 0000 0000 0000 1111 1111
               ----------------------------------------------
    AND Result: 0000 0000 0000 0000 0000 0000 0000 0000 (0)
  1. Beispiel mit /27 Präfix:
    image

Detaillierte Aufschlüsselung für /27:

Erstes Oktett (mask >> 27) & 0xff:
    Verschoben: 0000 0000 0000 0000 0000 0000 1111 1111
    0xFF:       0000 0000 0000 0000 0000 0000 1111 1111
               ----------------------------------------------
    AND Result: 0000 0000 0000 0000 0000 0000 1111 1111 (255)

Viertes Oktett (mask & 0xff):
    Original:   1111 1111 1111 1111 1111 1111 1110 0000
    0xFF:       0000 0000 0000 0000 0000 0000 1111 1111
               ----------------------------------------------
    AND Result: 0000 0000 0000 0000 0000 0000 1110 0000 (224)

Wichtige Punkte über & 0xFF:

  1. Zweck:

    • Extrahiert nur die letzten 8 Bits (ein Oktett) aus einer größeren Zahl
    • Stellt sicher, dass Werte im gültigen Bereich für ein IP-Adress-Oktett bleiben (0-255)
    • Maskiert unerwünschte Bits aus vorherigen Operationen

  2. Warum 0xFF?:

    • 0xFF ist in Binär 1111 1111 (8 Bits)
    • Bei AND-Verknüpfung mit einem beliebigen Wert:
      • Bleiben alle Bits in den letzten 8 Positionen erhalten
      • Werden alle anderen Bits auf 0 gesetzt
    • Perfekt für die Extraktion eines einzelnen Oktetts

  3. Im Kontext:

    • Nach der Rechtsverschiebung der Maske benötigen wir nur die letzten 8 Bits
    • Die & 0xFF Operation stellt sicher, dass wir genau diese 8 Bits erhalten
    • Dies ergibt Werte, die für die IP-Adressnotation geeignet sind

  4. Ergebnisse:

    • Produziert immer einen Wert zwischen 0 und 255
    • Perfekt geeignet für IP-Adress-Oktette
    • Behält das korrekte binäre Muster für die Subnetzmaske bei

  5. Häufige Muster:

    • & 0xFF ist ein Standardidiom in der Netzwerkprogrammierung
    • Wird oft in Verbindung mit Bit-Verschiebungen verwendet
    • Hilft bei der Einhaltung korrekter Byte-Grenzen
    • Wesentlich für die Aufschlüsselung von 32-Bit-Ganzzahlen in Oktette

Diese Kombination aus Rechtsverschiebung (>>) und AND (&) Operationen ermöglicht es uns, einzelne Oktette aus der 32-Bit-Subnetzmaske zu extrahieren und sie in die vertraute Punkt-Dezimal-Notation von IP-Adressen zu formatieren.

Bonus: Die XOR Operation

Die XOR-Operation ist eine weitere wichtige Bit-Operation, die vor allem in der Kryptographie, bei der Überprüfung von Checksummen sowie der Paritätenberechnung verwendet wird.

Ein weiteres weniger bekannte Beispiel ist beim Tausch der Werte zweier Variablen.

/**
 * XOR swap algorithm
 */
int x = 5;
int y = 3;
x = x ^ y; // x(5) ^ y(3)
y = y ^ x; // x(6) ^ y(3)
x = x ^ y; // x(3) ^ y(5)

Das besondere an dieser Technik ist, das keine temporäre Variable (Buffer) benötigt wird wie sonst üblich.

Anfangszustand:

x = 5  (binär: 101)
y = 3  (binär: 011)
  1. Erster Schritt: x = x ^ y

image

  1. Zweiter Schritt: y = y ^ x

image

  1. Dritter Schritt: x = x ^ y

image

Funktionsweise

  • XOR hat die besondere Eigenschaft, dass (a ^ b) ^ b = a
  • Diese Methode ist ein sehr effizienter Weg zwei Variablen zu tauschen, da weniger Operationen benötigt werden als einen Buffer zu deklarieren, zu initialisieren, ihn einen Wert zu zuweisen und diesen Wert in die zweite Variable zu kopieren.
  • Sie wird manchmal als "XOR swap" bezeichnet

Diese Methode ist zwar clever, aber in modernem Code verwendet man normalerweise die klassische Variante mit einer temporären Variable, da sie besser lesbar ist:

int temp = x;
x = y;
y = temp;

Verschiedene wichtige Anwendungsbereiche des XOR-Operators:

  1. Digitale Signatur: XOR wird in verschiedenen Signaturalgorithmen verwendet.

  2. Temporäre Datenverschleierung:

    • In Datenbanken
    • Bei der Übertragung sensibler Daten
    • In Speichersystemen

  3. Hardware-Design:

    • In logischen Schaltkreisen
    • Bei der Implementierung von Multiplexern
    • In FPGA-Designs

  4. Fehlerbehandlung:

    • RAID-Systeme nutzen XOR für Paritätsberechnungen
    • Fehlerkorrekturcodes in Speichermodulen (ECC-RAM)

  5. Netzwerksicherheit:

    • VPN-Protokolle
    • Tunnel-Verschlüsselung
    • Paketverarbeitung